Motivation
The dogma of game theory (and economics) is that strategic situations will reach equilibrium — one way or another. How this will happen is often left un-answered, but from a computational point of view this is quite a central question. Indeed, a great amount of work has been done regarding the computational complexity of reaching an equilibrium of a game, reaching a conclusion that an infeasible amount of computation might be needed. In this post I want to discuss another aspect of the complexity of reaching equilibrium: the amount of information that needs to be transferred between the different players. The point of view here is that initially each player “knows” only his own utility function  and then the players somehow interact until they find an equilibrium of the game
and then the players somehow interact until they find an equilibrium of the game  defined by their joint utilities. The analysis here abstracts away the different incentives of the players (the usual focus of attention in game theory) and is only concerned with the amount of information transfer required between the players. I.e., we treat this as a purely distributed computation question where the input
defined by their joint utilities. The analysis here abstracts away the different incentives of the players (the usual focus of attention in game theory) and is only concerned with the amount of information transfer required between the players. I.e., we treat this as a purely distributed computation question where the input  is distributed between the players who all just want to jointly compute an equilibrium point. We assume perfect cooperation and prior coordination between the players, i.e. that all follow a predetermined protocol that was devised to compute the required output with minimum amount of communication. The advantage of this model is that it provides lower bounds for all sorts of processes and dynamics and that eventually should reach equilibria: if even under perfect cooperation much communication is required for reaching equilibrium, then certainly whatever individual strategy each player follows, convergence to equilibrium cannot happen quickly.
is distributed between the players who all just want to jointly compute an equilibrium point. We assume perfect cooperation and prior coordination between the players, i.e. that all follow a predetermined protocol that was devised to compute the required output with minimum amount of communication. The advantage of this model is that it provides lower bounds for all sorts of processes and dynamics and that eventually should reach equilibria: if even under perfect cooperation much communication is required for reaching equilibrium, then certainly whatever individual strategy each player follows, convergence to equilibrium cannot happen quickly.
The main result that we shall give in this post is that finding a pure Nash equilibrium (or determining that none exists) requires essentially communicating everything about the utility functions — no shortcuts are possible. This is the basic result that appears in two papers that studied the issue: Communication complexity as a lower bound for learning in games by Vincent Conitzer and Tuomas Sandholm that considered two-player games and How Long to Equilibrium? The Communication Complexity of Uncoupled Equilibrium Procedures by Sergiu Hart and Yishay Mansour whose focus is multi-player games. See also the presentation by Sergiu Hart. A future post will discuss the much more complicated case of finding a mixed Nash equilibrium, a question which is still mostly open, despite results given in the H&M paper.
The Communication Complexity model
The basic communication complexity model considers  players, where each player
players, where each player  holds part of the input which we assume is an
holds part of the input which we assume is an  -bit string,
-bit string, 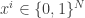 . The usual focus is on the two-player case,
. The usual focus is on the two-player case, 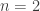 , in which case we simplify the notation to use
, in which case we simplify the notation to use  and
and  rather than
rather than 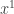 and
and 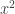 . The joint goal of these players is to compute the value of
. The joint goal of these players is to compute the value of  where
where  is some predetermined function. As
is some predetermined function. As  depends on all values of
depends on all values of 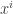 , the players will need to communicate with each other in order to do so (we will use “broadcasting” rather than player-to-player channels), and they will do so according to a predetermined protocol. Such a protocol specifies when each of them speaks and what he says, where the main point is that each player’s behavior must be a function of his own input as well as what was broadcast so far. We will assume that all communication is in bits (any finite alphabet can be represented in bits). The communication complexity of
, the players will need to communicate with each other in order to do so (we will use “broadcasting” rather than player-to-player channels), and they will do so according to a predetermined protocol. Such a protocol specifies when each of them speaks and what he says, where the main point is that each player’s behavior must be a function of his own input as well as what was broadcast so far. We will assume that all communication is in bits (any finite alphabet can be represented in bits). The communication complexity of  is the minimum amount of bits of communication that a protocol for
is the minimum amount of bits of communication that a protocol for  uses in the worst case. This model has been introduced in a seminal paper by Andy Yao, the standard reference is still the (just slightly dated) book Communication Complexity I wrote with Eyal Kushilevtiz, and online references include the wikipedia article, and the chapter from the Barak-Arora computational complexity book.
uses in the worst case. This model has been introduced in a seminal paper by Andy Yao, the standard reference is still the (just slightly dated) book Communication Complexity I wrote with Eyal Kushilevtiz, and online references include the wikipedia article, and the chapter from the Barak-Arora computational complexity book.
.
The Disjointness Function
Our interest will be in lower bounds on the communication complexity. There are several techniques known for proving such lower bounds, the easiest of which is the “fooling set method” which we will use on the “disjointness function” for two players. The disjointness function, introduced in Yao’s original paper, plays a key role in communication complexity, and indeed it will turn out to be useful to us too: once we have a lower bound for it, it will be easy to easily deduce the lower bound for the function of our interest, finding a pure Nash equilibrium, by simple reduction.
The disjointness function: Alice holds  and Bob holds
and Bob holds 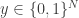 . They need to determine whether there exists an index
. They need to determine whether there exists an index  where they both have 1,
where they both have 1, 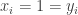 . If we view
. If we view  as specifying a subset
as specifying a subset  and
and  as specifying
as specifying 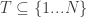 , then we are asking whether
, then we are asking whether  .
.
Lemma: Any deterministic protocol for solving the disjointness problem requires at least  bits of communication in the worst case.
bits of communication in the worst case.
Before proving this lemma, notice that it is almost tight, as Alice can always send all her input to Bob ( bits) who then has all the information for determining the answer, who then sends it back to Alice (1 more bit). It is known that a
bits) who then has all the information for determining the answer, who then sends it back to Alice (1 more bit). It is known that a  lower bound also applies to randomized protocols, but the proof for the randomized case is harder, while the proof for the deterministic case is easy.
lower bound also applies to randomized protocols, but the proof for the randomized case is harder, while the proof for the deterministic case is easy.
Proof: Let us look at the 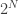 different input pairs of the form
different input pairs of the form  (these are the “maximal disjoint” inputs). We will show that for no two of these input pairs can the protocol produce the same communication transcript (i.e. the exact same sequence of bits is sent throughout the protocol). It follows that the protocol must have at least
(these are the “maximal disjoint” inputs). We will show that for no two of these input pairs can the protocol produce the same communication transcript (i.e. the exact same sequence of bits is sent throughout the protocol). It follows that the protocol must have at least 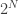 different possible transcripts, and since these are all binary sequences, at least one of them must be of length at least
different possible transcripts, and since these are all binary sequences, at least one of them must be of length at least  bits.
bits.
Now comes the main point: why can’t two maximally disjoint pairs 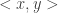 and
and 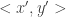 have the same transcript? Had we been in a situation that
have the same transcript? Had we been in a situation that 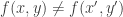 then we would know that the transcripts must be different since the protocol must output a different answer in the two cases; however in our case all “maximal disjoint” input pairs give the same answer: “disjoint”. We use the structure of communication protocols — that each player’s actions can only depend on his own input (and on the communication so far) — to show that if
then we would know that the transcripts must be different since the protocol must output a different answer in the two cases; however in our case all “maximal disjoint” input pairs give the same answer: “disjoint”. We use the structure of communication protocols — that each player’s actions can only depend on his own input (and on the communication so far) — to show that if 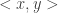 and
and 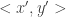 have the same transcript then
have the same transcript then 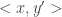 has the same transcript too (and so does
has the same transcript too (and so does  ). Consider the players communicating on inputs
). Consider the players communicating on inputs 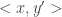 : Alice, that only sees
: Alice, that only sees  , cannot distinguish this from the case of
, cannot distinguish this from the case of 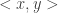 and Bob, that only sees
and Bob, that only sees 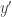 cannot distinguish it from the case
cannot distinguish it from the case 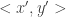 . Thus when Alice communicates she will not deviate from what she does on of
. Thus when Alice communicates she will not deviate from what she does on of 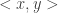 and Bob will not deviate from what he does on
and Bob will not deviate from what he does on 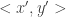 . Thus, none of them can be the first to deviate from the joint transcript, thus none of them ever does deviate and the joint transcript is also followed on
. Thus, none of them can be the first to deviate from the joint transcript, thus none of them ever does deviate and the joint transcript is also followed on 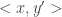 . We now get our contradiction since either
. We now get our contradiction since either  and
and 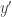 are not disjoint or
are not disjoint or 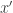 and
and  are not disjoint, and thus at least one of these pairs cannot not share the same transcript, a contradiction. (The reason for non disjointness is that since
are not disjoint, and thus at least one of these pairs cannot not share the same transcript, a contradiction. (The reason for non disjointness is that since 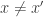 there must be an index
there must be an index  with
with 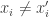 . If
. If  and
and 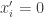 then
then  and
and 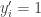 in which case
in which case  and
and 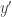 are not disjoint. Similarly, if
are not disjoint. Similarly, if  and
and  then
then 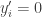 and
and 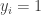 in which case
in which case 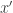 and
and  are not disjoint.)
are not disjoint.)
Finding a Pure Nash Equilibrium
Back to our setting where each player  holds his own utility function
holds his own utility function  , where the
, where the 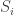 ‘s are the commonly known strategy sets, which we will assume have size
‘s are the commonly known strategy sets, which we will assume have size  each. Thus each player’s input consists of
each. Thus each player’s input consists of  real numbers, which we will always assume are in some small integer range. Perhaps it is best to start with a non-trivial (just) upper bound. Let us consider the class of games that are (strictly) dominance solvable, i.e. those that iterated elimination of strictly dominated strategies leaves a single strategy profile, which is obviously a pure Nash equilibrium. A simple protocol to find this equilibrium is the following:
real numbers, which we will always assume are in some small integer range. Perhaps it is best to start with a non-trivial (just) upper bound. Let us consider the class of games that are (strictly) dominance solvable, i.e. those that iterated elimination of strictly dominated strategies leaves a single strategy profile, which is obviously a pure Nash equilibrium. A simple protocol to find this equilibrium is the following:
- Repeat
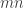 times:
times:
- For
 do
do
- If player
 has a strategy that is dominated after the elimination of all previously removed strategies, then announce it, else say “pass”.
has a strategy that is dominated after the elimination of all previously removed strategies, then announce it, else say “pass”.
- Output the (single) profile of non-eliminated strategies.
What is remarkable about this protocol is that number of bits communicated is polynomial in  and
and  , which may be exponentially smaller than the total size of the input which is
, which may be exponentially smaller than the total size of the input which is  numbers for each player. Can some protocol like this be designed for all games that have a pure Nash equilibrium? The basic answer in no:
numbers for each player. Can some protocol like this be designed for all games that have a pure Nash equilibrium? The basic answer in no:
Theorem: Every deterministic (or randomized) protocol that recognizes whether the given game has a pure Nash equilibrium requires  bits of communication.
bits of communication.
Note that this theorem implies in particular that one cannot design a more efficient protocol that finds an equilibrium just for games that are guaranteed to have one, as adding a verification stage (where each player checks whether the strategy suggested to him is indeed a best reply to those suggested to the others) would convert it to a protocol that recognizes the existence of a pure Nash.
Proof: The proof is by a reduction from the disjointness problem. We will show that a protocol for determining the existence of a pure Nash equilibrium for games with  players each having
players each having  strategies can be used to solve the disjointness problem on strings of length
strategies can be used to solve the disjointness problem on strings of length  .
.
Let us start with the case 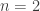 and solve disjointness for length
and solve disjointness for length 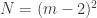 . The idea is very simple: Alice will build a utility matrix
. The idea is very simple: Alice will build a utility matrix  by filling it with the values of its bit string
by filling it with the values of its bit string  in some arbitrary but fixed order, and Bob will build a matrix
in some arbitrary but fixed order, and Bob will build a matrix 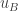 from
from  using the same order. Now, any cell of the two matrices where
using the same order. Now, any cell of the two matrices where 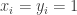 will turn out to be a Nash equilibrium since both players get the highest utility possible in this matrix. For this idea to formally work, we just need to make sure that no other cell is a Nash equilibrium. This can be done in one of several ways (and different ones are used in the C&S and H&M papers), the simplest of which is adding two more rows and columns as follows:
will turn out to be a Nash equilibrium since both players get the highest utility possible in this matrix. For this idea to formally work, we just need to make sure that no other cell is a Nash equilibrium. This can be done in one of several ways (and different ones are used in the C&S and H&M papers), the simplest of which is adding two more rows and columns as follows:

With the addition of these rows and columns, each player’s best-reply always obtains a value of 1, and thus only a (1,1) entry may be a Nash equilibrium.
Now for general  . We add to Alice and Bob
. We add to Alice and Bob 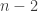 players that have utilities that are identically 0. Thus any strategy will be a best reply for these new players, and a pure Nash equilibrium is determined solely by Alice and Bob. The main change that the new players bring is that the utility functions of Alice and Bob are now
players that have utilities that are identically 0. Thus any strategy will be a best reply for these new players, and a pure Nash equilibrium is determined solely by Alice and Bob. The main change that the new players bring is that the utility functions of Alice and Bob are now  -dimensional matrices of total size
-dimensional matrices of total size  . Thus Alice and Bob can fold their length
. Thus Alice and Bob can fold their length  bit string into this larger table (as before keeping two strategies from their own strategy space to ensure no “none-(1,1)” equilibrium points), allowing to answer disjointness on
bit string into this larger table (as before keeping two strategies from their own strategy space to ensure no “none-(1,1)” equilibrium points), allowing to answer disjointness on  -bit long vectors.
-bit long vectors.
Variants
There are several interesting variants on the basic question:
- The lower bound uses heavily the fact that the utilities of different strategies may be equal and thus there are many possible best replies. Would finding a Nash equilibrium be easier for games in “general position” — specifically if there was always a single best reply for each player? For the case of
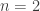 players, C&S show that the complexity does go down to
players, C&S show that the complexity does go down to  . (Exercise: show that the randomized communication complexity in this case is
. (Exercise: show that the randomized communication complexity in this case is 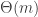 .) As
.) As  grows, the savings are not exponential though and H&M show a
grows, the savings are not exponential though and H&M show a 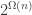 lower bound for constant
lower bound for constant  . A small gap remains.
. A small gap remains.
- We have seen that finding an equilibrium of a dominance solvable game is easy. Another family that is guaranteed to posses a pure equilibrium is potential games. However, H&M show that finding a Nash equilibrium in an ordinal potential game may require exponential communication. I don’t know whether things are better for exact potential games.
- The efficient protocol for dominance solvable games was certainly artificial. However, an efficient natural protocol exists as well: if players just best reply in round robin fashion then they will quickly converge to a pure Nash equilibrium. (This seems to be well known, but the only link that I know of is to one of my papers.)
Read Full Post »
