The basic computational problem in algorithmic game theory is that of computing a (mixed) Nash equilibrium of a given (non-cooperative) game. The computational complexity status of this problem has been recently settled by showing that it is “PPAD-complete” and thus “unlikely” to be efficiently computable (see this link for a nice overview). This may be considered as not very satisfying answer due to our incomplete understanding of the class PPAD, but at least the problem is now reduced to be a purely computational complexity one with no game theory aspects to it and no special role for the Nash problem. The main related problem remaining is whether approximating a Nash equilibrium may be done efficiently. This post will describe the current status of the approximation problem.
The approximate-Nash problem
Let us first settle on some notation. We are talking about a 
-player game, where each player 
has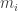 
possible strategies, each player has a utility function 
. We will denote by 
the set of probability distributions on 
and for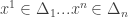 
we use 
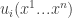as a shorthand for 
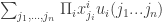, the expected value of 
where each 
is chosen at random according to the probability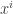 
.
We know by Nash’s theorem that a mixed Nash equilibrium of the game exists and the computational problem is to find one. Unfortunately, it is also known that when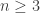 
then the Nash equilibria may all be irrational numbers. We thus cannot just ask our algorithm to output a Nash equilibrium since it may not have a finite representation and so we need to settle for approximation in order to even define the “exact” problem. So here is the carefully stated common definition of the Nash equilibrium computation problem:
Input: The input is given by tables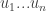 
each of dimensions 
. For finiteness of representation, each of the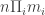 
numbers in the input is a rational number given by a 
-digit numerator and denominator. We are also give a rational number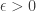 
(with -digit numerator and denominator).
Output: rational vectors 
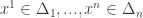that are an 
-Nash equilibrium.
Definition: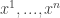 
are -Nash of the game defined by 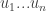if for every and every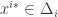 
we have that 
.
Running time: we want the running time to be polynomial in the input size, i.e. polynomial in , , and 
.
It is quite useful to look carefully at various choices made here, and what we would get with slightly different choices:
- Allowing any Nash equilibrium: our definition allowed any ()-Nash rather than specifying which one we desire in case multiple ones exist. It is known that most ways of attempting to require a specific Nash point make the problem harder, NP-complete.
- Approximation: as mentioned above when 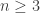we need to settle for a -approximation just to have a finite output. For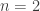
there always exists an equilibrium which has rational numbers with 
-digit long numerator and denominator, and thus the exact version is equivalent to the problem as stated.
- Approximation of best-response condition: our notion for approximation relaxed the best-response condition by rather than asking for some rational point that is -close to an exact Nash equilibrium point. The latter condition seems to be much harder and in not even known to be in NP (or in fact even in the polynomial time hierarchy) and is treated at length by this 57-page paper by Mihalis Yannakakis and Kousha Etessami. The crux of the difficulty is that getting some grip on an exact Nash point seems to require “infinite precision” arithmetic — the same type of problem encountered in trying to determine whether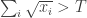
(discussed by Richard Lipton and see also this related post of his). (Thanks to Kousha Etessami for explaining these delicate issues to me.)
- Having be given in binary: in our definition was given by -digit numerator and denominator and the running time was required to be polynomial in , i.e. in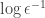
. An alternative version would be to require to be “given in unary” i.e. allow the algorithm to run in time polynomial in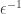 
. This version is asking for a fully polynomial approximation scheme (FPTAS) and could be easier. However, it turns out that getting a FPTAS is also PPAD-hard and thus this is actually not the case.
- Additive approximation: Our condition demands . We can not use the more natural relative error
as the Nash equilibrium point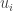 
may be arbitrarily close to zero which may again require an exponential-length answer.
At this point we can start talking about the approximate version of this problem. For this we will allow an arbitrary dependence of the running time on and even allow be fixed (e.g.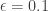 
) . As the original problem scales, for the approximation to make sense, we need to normalize by the sizes of the numbers in the probem.
-Approximation Problem: This is the same problem as above but scaled so that the utilities all satisfy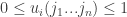 
.
A Quasi-polynomial-time Algorithm
The key result by Richrad Lipton, Evangelos Marakakis, and Aranyak Metha is that the approximation problem can be solved in “quasi-polynomial” time — in this case time 
where 
is the input size. The algorithm is very simple and is based on the existence of approximate equilibria with strategies that have only small support. In many “non-uniform” models, randomization over a large domain can be replaced by randomization over a much smaller domain. (One nice example is the simulation of public coins by private ones in communication complexity.) This is the situation here and some background is given in a recent blog post by Richard Lipton.
Definition: Let 
be an integer, then a distribution 
is -simple if all its coordinates are integer multiples of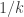 
. I.e. it is a uniform distribution on a multi-set of size of pure strategies. A random -simplification of 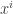is obtained by choosing at random elements (with repetitions) according to the distribution specified by 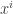and then taking the uniform distribution on this multiset.
Proposition: For every 
and fixed pure strategies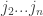 
, if we chose a random -simplification 
of 
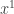then ![Pr[|u_i(\tilde{x}^1,j_2,...,j_n) - u_i(x^1,j_2,...,j_n)| > \epsilon] \le e^{-\Omega(k\epsilon^2)}](https://s0.wp.com/latex.php?latex=Pr%5B%7Cu_i%28%5Ctilde%7Bx%7D%5E1%2Cj_2%2C...%2Cj_n%29+-+u_i%28x%5E1%2Cj_2%2C...%2Cj_n%29%7C+%3E+%5Cepsilon%5D+%5Cle+e%5E%7B-%5COmega%28k%5Cepsilon%5E2%29%7D&bg=ffffff&fg=333333&s=0&c=20201002)
.
The proof is by observing that 
is the expected value of 
when 
is chosen according to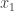 
, while 
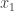is the average value of over random choices of according to , and thus the proposition is just a direct use of the Hoeffding tail inequalities.
Now, if we choose 
, where 
, then, with high probability (due to the union bound), the previous proposition holds for all pure strategies 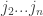and all 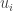for 
. In this case, by averaging, it also holds for all mixed strategies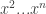 
:
Definition: 
is an -approximation of 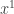(relative to 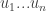) if for all 
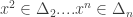and all we have 
.
Corollary: For every there exists an -approximation which is -simple, for .
The main lemma now follows:
Lemma: Every game has an -Nash equilibrium where all player strategies are -simple, with .
The proof starts with any Nash equilibrium 
and chooses a -simple 
-approximation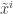 
for each 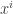(where 
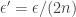). Since are an exact Nash equilibrium, in order to show that 
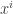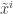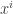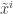are an approximate equilibrium, it suffices to show that changing the ‘s to ‘s changes things by at most — but this is exactly what being an -approximation means for replacing a single by , and the approximation errors ‘s simply add up.
Once the existence of a -simple -equilibrium is known, an 
algorithm follows simply by exhaustive search, and thus we get our algorithm.
Notice that we have actually shown a stronger theorem: not only can we find some -approximation but in fact we can find an approximation to any equilibrium, and our approximated equilibrium maintains also player’s utilities. This for example also provides an approximate equilibrium with approximately optimal social welfare.
A polynomial time algorithm?
The existence of a quasi-polynomial time algorithm may often be viewed as a hint that a polynomial-time algorithm exists as well. In our case the main open problem is whether such a polynomial time algorithm exists for every fixed value of 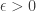. The upper bounds for the approximation problem are rater weak and the best that is known is a polynomial time approximation for 
.
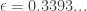One possible approach is to see whether the parameter above may be reduced to being constant when is constant. This however is not the case. Consider a zero-sum two-player game where each utility is chosen at random to be 0 or 1. The following statements can be easily shown to hold with high probability over the random choice of the game: (a) for each row or column, the fraction of 1-entries is very close to 1/2 and thus a value of close to 1/2 can be obtained by any player by using a uniform distribution on his rows or columns (b) for any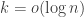 
rows there exists a single column which has all 0 entries in these rows. Thus any mixed strategy that is 
-simple cannot ensure positive value. It follows that there does not exists a -approximate Nash which is -simple for any 
and 
. A recent paper of Constantinos Daskalakis and Christos Papadimitriou generalizes this impossibility not only to simples strategies but to more general “oblivious” algorithms.
Another difficulty is shown by a recent paper of Elad Hazan and Robert Krauthgamer. They consider the harder problem of approximating a specific Nash equilibrium — specifically the one with highest social welfare — for which the technique above also provides a quasi-polynomial-time algorithm. They show that this problem is at least as hard as the known problem of finding a small randomly planted clique in a graph, providing some evidence for its difficulty.
Read Full Post »
approximation by adding a distributional assumption to model.
Turing's Invisible Hand 
